判異準則有二類：

(1) 點子出界(包括壓線)就判異；

(2) 界內點排列不隨機則判異。(原則上有無窮多種)。

模式1  點子屢屢接近管制界限

此模式中，『接近』系指距離管制界限在1s范圍內(下圖為3點中有2點接近管制界限判異)。

此時屬下列情況的，點子排列不隨機判異：

(1) 連續3點中，至少有2點接近管制界限；

(2) 連續7點中，至少有3點接近管制界限；

(3) 連續10點中，至少有4點接近管制界限。

模式2  鍵

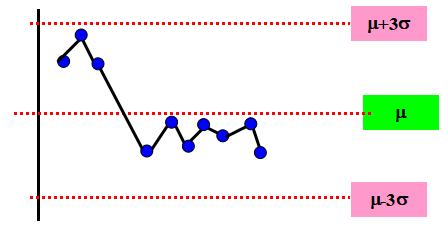
上圖表示質量特性值分布的平均值m向出現鍵的一側偏移(7點鍵)。

(1) 在管制圖中心線一側連續出現的點稱為鍵，其中包含的點子數目稱為鍵長。當鍵長3 9，則判異。

(2) 分析其a，

P(中心線一側出現長為9的鍵)

= 2*(0.9973/2)^9 = 0.0038 = a9

P(中心線一側出現長為7的鍵)

= 2*(0.9973/2)^7 = 0.0153 = a7

a7 / a9 = 4

過去采7點鍵判異。目前多國改采9點鍵判異。

模式3  間斷鍵

間斷鍵是指鍵中個別點子跳到中心線的另一側的鍵。

(1) 連續11點中，至少有10點在一側；(下圖)

(2) 連續14點中，至少有12點在一側；

(3) 連續17點中，至少有14點在一側；

(1) 連續20點中，至少有16點在一側。

依機率計算，上述四條判異準則的顯著性水平分別為：

a1 = 1.14%    a2 =1.25%

a3 =1.22%       a4 =1.12%

由判異準則知，其(四種狀況) a 分別均大于0.01，偏大，建議不予使用，除非增加判異準則中的點子數目。

模式4  傾向

下圖示中出現有下降傾向(7點下降傾向)，表下品質特性值分布的平均值m 隨時間而減少。點子遞增或遞減的狀態稱之傾向或趨勢。

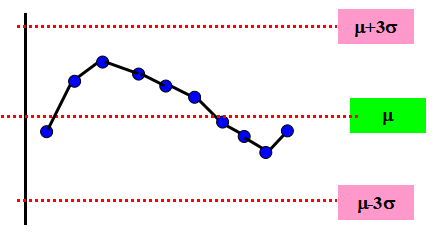
◎ 下降(上升)傾向，后面的點子一定要低(高)于或等于前面的點子，否則傾向中斷，須重新起算。

◎ 過去為7點傾向判異，即連續7點上升或下降則判異。目前改為6點傾向判異。

證明：  P(n點傾向) = [2(0.9973)^n] /n!

P(5點傾向) = [2(0.9973)^5] /5!= 0.01644 = a5

P(6點傾向) = [2(0.9973)^6] /6!= 0.00273 = a6

P(7點傾向) = [2(0.9973)^7] /7!= 0.00039 = a7

由于a6 = 0.00273，最接近謝華特的a0= 0.0027，故6點傾向判異是合適的。

模式5  點子集中在中心線附近

◎ 『中心線附近』即指『中心線附近±1s的范圍內』。

◎ 下圖的現象表示質量特性值分布的標準差s減小。切記此現象亦可能異常，須檢查下列二種情況：

(1) 是否應用了假數據，有弄虛作假現象；

(2) 是否分層不夠。

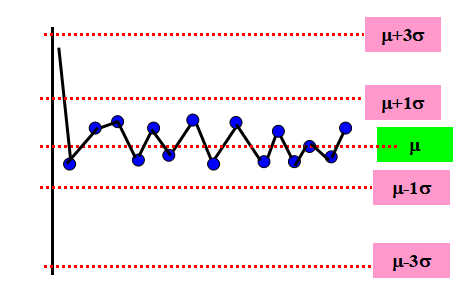
依機率計算：

連續14、15、16個點集中在中心線附近的a為

a14 = 0.68268^14 = 0.00478

a15 = 0.68268^15 = 0.00326

a16 = 0.68268^16 = 0.00223

※ 模式5的 a 取為a15 = 0.00326，比較接近判異準則(1)的a0 = 0.0027。

模式6  點子作周期性變化

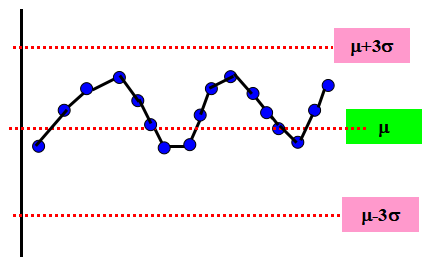
◎ 下圖的現象表示點子呈周期性變化。產生其原因有下列二種情況：

(1) 操作人員疲勞；(2) 原材料發送有問題

(3) 熱累積或應力累積。

※消除上述周期性變化可使產品質量更加穩定。